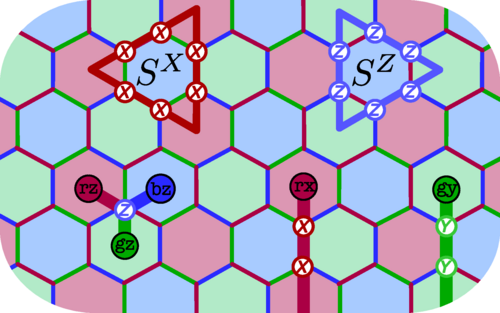
Illustration of the hexagonal color code on a qubit lattice, showing the creation of anyons and their fusion rules, with examples of how string operators generate bosonic anyons along colored edges. (see figure 2 of the paper)
New Quantum Error Correction Code Published in PRX Quantum
In a collaboration of the team of Markus Müller at RWTH Aachen and FZJ with Jens Eisert’s group in Berlin, the team has completed a new work in quantum error correction, published in PRX Quantum: The work presents a new highly attractive Floquet-type quantum error correcting code, and introduce – yet another – useful graphical calculus.
Analyzing and developing new quantum error-correcting (hashtagQEC) schemes is one of the most prominent tasks in quantum computing research. In such efforts, introducing time dynamics explicitly in both analysis and design of error-correcting protocols constitutes an important cornerstone. In this work, the authors present a graphical formalism based on tensor networks to capture the logical action and error-correcting capabilities of any Clifford circuit with Pauli measurements.
They showcase the functioning of the formalism on new Floquet codes derived from topological subsystem codes, which they call XYZ ruby codes. Based on the projective symmetries of the building blocks of the tensor network they develop a framework of Pauli flows. Pauli flows allow for a graphical understanding of all quantities entering an error-correction analysis of a circuit, including different types of QEC experiments, such as memory and stability experiments. They lay out how to derive a well-defined decoding problem from the tensor-network representation of a protocol and its Pauli flows alone, independent of any stabilizer code or fixed circuit. Importantly, this framework applies to all Clifford protocols and encompasses both measurement-based and circuit-based approaches to fault tolerance.
The method is applied to a new family of dynamical codes, which are in the same topological phase as the 2+1-dimensional color code, making them a promising candidate for low-overhead logical gates. In contrast to its static counterpart, the dynamical protocol applies a ℤ₃ automorphism to the logical Pauli group every three time steps. The authors highlight some of its topological properties and comment on the anyon physics behind a planar layout. Lastly, they benchmark the performance of the XYZ ruby code on a torus by performing both memory and stability experiments and find competitive circuit-level noise thresholds of approximately equal to 0.18%, comparable with other Floquet codes and 2+1-dimensional color codes.
Publication: XYZ Ruby Code: Making a Case for a Three-Colored Graphical Calculus for Quantum Error Correction in Spacetime. Julio C. Magdalena de la Fuente, Josias Old, Alex Townsend-Teague, Manuel Rispler, Jens Eisert, and Markus Müller. PRX Quantum 6, 010360 – Published 28 March, 2025
DOI: https://doi.org/10.1103/PRXQuantum.6.010360
