Advancing Quantum Error Correction: New Threshold Estimation Method
A joint study between M. Müller’s and S. Diehl’s groups appears today in Physical Review Research introducing a novel method for accurately estimating error thresholds in quantum error correcting codes, enhancing the potential for robust quantum systems.
In a collaborative effort between S. Diehl’s and M. Müller’s research groups, a recent publication titled “Accurate Optimal Quantum Error Correction Thresholds from Coherent Information“ presents an innovative approach to estimating fundamental error thresholds across a wide range of quantum error correcting codes and error processes. This new method focuses on calculating the coherent information of quantum states—essentially quantifying the actual quantum information contained in noisy qubits.
By applying this technique to common scenarios encountered in current quantum devices, the research not only demonstrates its effectiveness but also paves the way for further advancements in the methodology. The ability to accurately determine error thresholds is crucial for enhancing the reliability and performance of quantum error correction, ultimately contributing to the development of more resilient quantum computing systems. This work represents a significant step forward in our understanding of quantum information dynamics and holds promise for future innovations in the field.
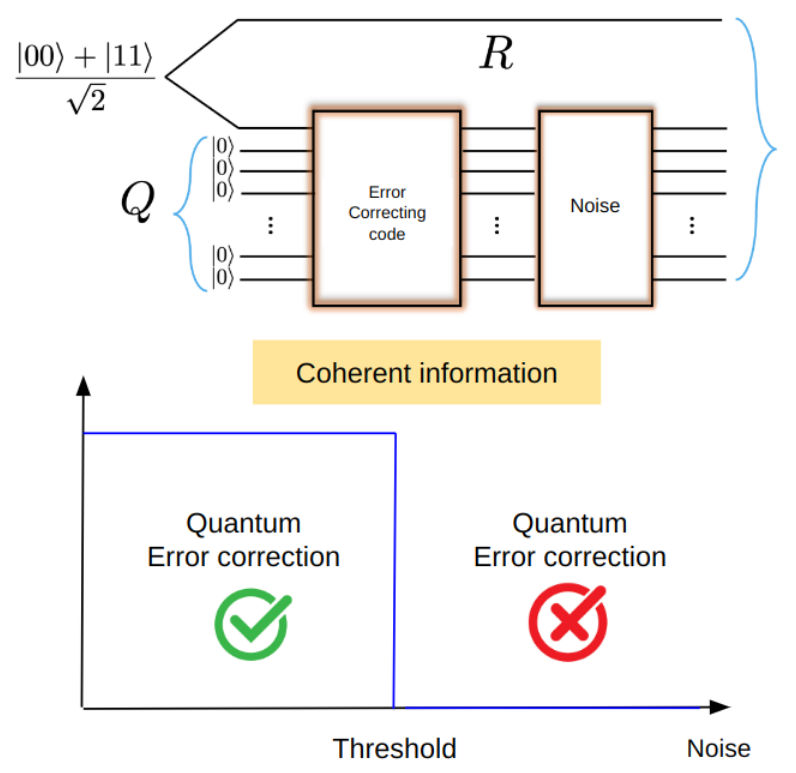
The study of the coherent information of noisy quantum error correcting codes provides an alternative route to reveal information about the fundamental thresholds, below which successful quantum error correction becomes possible [see Figure 1 of the publication].
Publication:
Accurate optimal quantum error correction thresholds from coherent information. Luis Colmenarez, Ze-Min Huang, Sebastian Diehl, and Markus Müller. Phys. Rev. Research 6, L042014 – Published 15 October 2024
DOI: https://doi.org/10.1103/PhysRevResearch.6.L042014
