New paper in Nature Physics: Nishimori transition across the error threshold for constant-depth quantum circuits

Guo-Yi Zhu from Simon Trebst’s group at the University of Cologne, in collaboration with IBM Quantum, demonstrated the generation of long-range order—specifically, Ising order—on a 54-qubit quantum processor. Using a novel measurement-based protocol, the team identified hidden order in the system despite noise and imperfections. Crucially, they discovered that a rare phase transition, tied to the Nishimori universality class, arises naturally from the fundamental rules of quantum mechanics (Born rule for measurement probabilities). This finding not only sheds light on the stability of quantum states in the presence of noise but also opens new avenues to explore complex physics at scales beyond 100 qubits.

Publication: Chen, E.H., Zhu, GY., Verresen, R. et al. Nishimori transition across the error threshold for constant-depth quantum circuits. Nat. Phys. (2024). https://doi.org/10.1038/s41567-024-02696-6

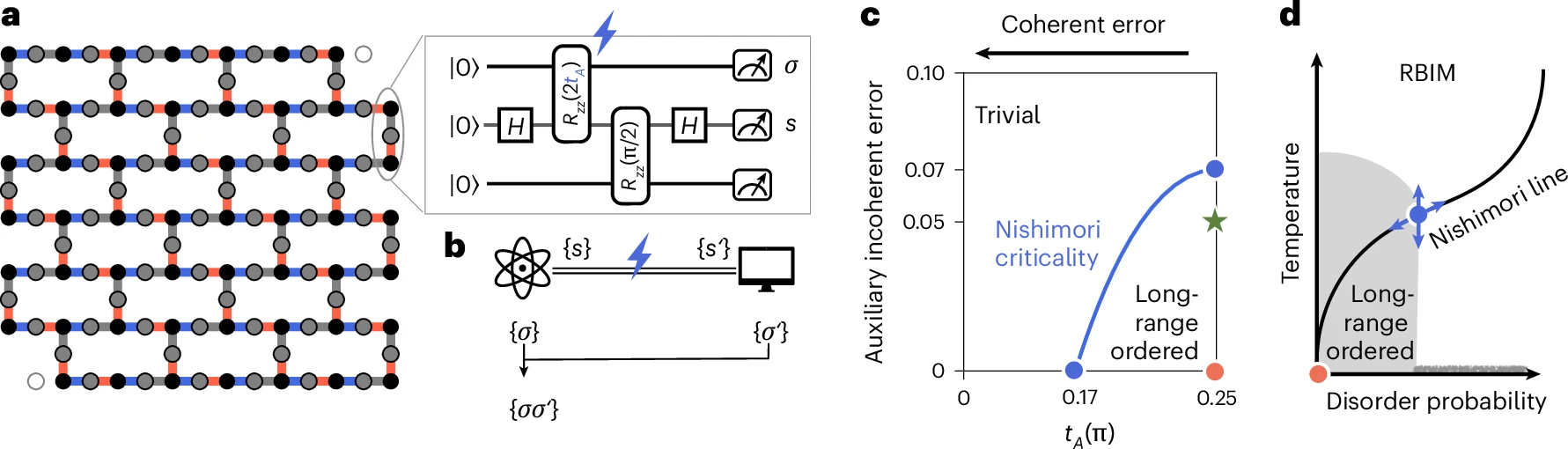
a, The heavy-hexagonal lattice of 127 qubits. For the 125 active qubits, the inset shows the building block using constant-depth entangling circuits for the three nearest neighbours (grey circles) of each system qubit (black circles) in the presence of noise (blue lightning). The RZZ gates are executed in order from blue, red then grey bonds within three layers. The auxiliary outcomes, s, on the bonds of the lattice (grey) can be used to inform a decoder for the data outcomes, σ, on the vertices of the lattice (black). b, The quantum device outputs a data bit-string {σ} together with an auxiliary outcome {s}. In the presence of noise, the auxiliary outcomes become before being passed to a classical decoder to determine a classical replica of the bit-string . Their element-wise product, , serves as the decoded bit-string. A measurement error (blue lightning) can corrupt the communication channel between the quantum replica and the classical replica. c, The trivial and long-range ordered phases sweep out distinct regions depending on the strength of coherent and incoherent noise. Within a finite threshold, a stable phase (grey), of which the GHZ state is a special case (red circle), exhibits long-range entanglement in the absence of other sources of noise (for example, without dephasing). Even in the presence of dephasing (not shown), classical long-range ordering remains. The boundary separating the trivial and long-range phases is described by the Nishimori criticality. Our experiments have incoherent error rates as low as ~0.05, which is indicated by the green star. d, A schematic phase diagram of the classical RBIM. The solid black line is the Nishimori line, which captures the entire phase diagram in c. [Source: Nature, Fig. 1 as published in the paper]

Abstract: Quantum computing involves the preparation of entangled states across many qubits. This requires efficient preparation protocols that are stable to noise and gate imperfections. Here we demonstrate the generation of the simplest long-range order—Ising order—using a measurement-based protocol on 54 system qubits in the presence of coherent and incoherent errors. We implement a constant-depth preparation protocol that uses classical decoding of measurements to identify long-range order that is otherwise hidden by the randomness of quantum measurements. By experimentally tuning the error rates, we demonstrate the stability of this decoded long-range order in two spatial dimensions, up to a critical phase transition belonging to the unusual Nishimori universality class. Although in classical systems Nishimori physics requires fine-tuning multiple parameters, here it arises as a direct result of the Born rule for measurement probabilities. Our study demonstrates the emergent phenomena that can be explored on quantum processors beyond a hundred qubits.

Previous related publication highlights