Quantum computers to test for the first time Jarzynski’s equality for many interacting particles
Joint efforts including the Luitz (Bonn) and Rizzi (Cologne/Jülich) Groups yield results published in Physical Review X earlier this month
Statistical mechanics is a branch of physics that uses statistical and probabilistic methods to understand the behavior of a large number of microscopic particles, such as atoms and molecules, in a system. Instead of focusing on the individual motion of each particle, statistical mechanics analyzes the collective properties of the system. It provides a bridge between the microscopic world of particles and the macroscopic world we can observe, explaining phenomena like the behavior of liquids and gases, phase transitions, and the thermodynamic properties of materials. Through the statistical distribution of particle properties, such as energy and velocity, statistical mechanics helps us make predictions about how physical systems behave on a larger scale, contributing to our understanding of fundamental principles in physics and chemistry.
One of the most remarkable relations in statistical mechanics is the Jarzynski equality, connecting the irreversible work performed in an arbitrary thermodynamic process with the energy and entropy of the system in thermodynamic equilibrium. Because the system is free to leave the equilibrium state during its evolution, Jarzynski’s equality is a prime example of how equilibrium physics can constrain the outcome of nonequilibrium processes. Remarkably, the familiar Second law of Thermodynamics – a fundamental principle of physics – follows directly from Jarzynski’s equality. The Second law is a statement about the average properties of particles in a system undergoing a thermodynamic process, and postulates that heat always flows spontaneously from hotter to colder regions of the system. Intriguingly, Jarzynski’s equality shows that this fundamental law of Thermodynamics can be “violated” in individual realizations of a process (but never on average!).
Despite its fundamental importance, experimental tests of Jarzynski’s equality for classical and quantum systems are extremely challenging, since they require complete control in manipulating and measuring the system. Even more so, a test for many quantum interacting particles was until recently completely missing.
In a new joint study, an international team from the Max Planck Institute for the Physics of Complex Systems, the University of California at Berkeley, the Lawrence Berkeley National Laboratory, the German Cluster of Excellence ML4Q and the Universities of Cologne, Bonn, and Sofia identified quantum computers as a natural platform to test the validity of Jarzynski’s equality for many interacting quantum particles. (A quantum computer is a computing device that uses the principles of Quantum Mechanics to perform certain types of calculations at speeds and efficiency levels that are unattainable by classical computers. Quantum computers use quantum bits, or qubits, as the basic unit of information. Hence, any quantum computer is, at its core, a system of interacting quantum particles.)
The researchers used the quantum bits of the quantum processor to simulate the behavior of many quantum particles undergoing nonequilibrium processes, as is desired for an experimental verification of Jarzynski’s equality. They tested this fundamental principle of nature on multiple devices and using different quantum computing platforms. To their surprise, they found that the agreement between theory and quantum simulation was more accurate than originally expected due to the presence of computational errors, which are omnipresent in current quantum computers. The obtained results demonstrate a direct link between certain types of errors that can occur during quantum computations, and violations of Jarzynski’s equality, revealing a fascinating connection between quantum computing technology and this fundamental principle of physics.
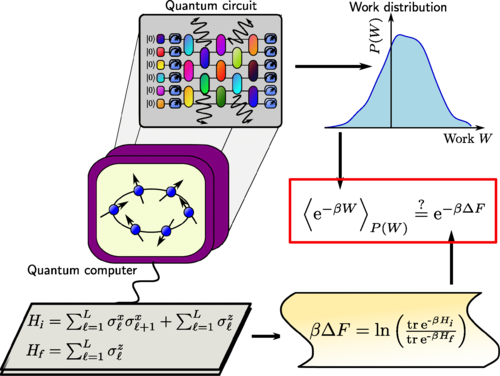
Schematics of the protocol to test the quantum Jarzynski equality in the quantum many-body regime as proposed by Hahn et al. in Phy.Rev.X (https://doi.org/10.1103/PhysRevX.13.041023; Figure 1): The authors simulate the dynamics of a system of interacting qubits initiated in a thermal state of the transverse-field Ising chain H_i. The qubits then evolve under a nonequilibrium process on a quantum computer affected by energy dissipation. Finally, they extract the work distribution for the quantum circuit with respect to the final Hamiltonian H_f. At the same time, they independently compute the exact theory prediction for the free energy difference. They compare both results against each other to test the validity of Jarzynski’s equality (red box).
Publication:
Dominik Hahn, Maxime Dupont, Markus Schmitt, David J. Luitz, and Marin Bukov, Physical Review X 13, 041023 (2023)
DOI: https://doi.org/10.1103/PhysRevX.13.041023