Qubit fractionalization and emergent Majorana liquid in the honeycomb Floquet code induced by coherent errors and weak measurements
Use the slider to read the story of this paper as Simon Trebst summarizes it in 6 images:
In quantum error correction, stabilizer codes using a set of *commuting* measurements (such as the toric code or surface code) have been the go-to solution for topological quantum memories — despite the need for multi-qubit measurements.
Introducing Floquet codes, Hastings & Haah showed that one can bring this down to two-qubit checks and dynamically stabilize logical qubits but at the cost of using *non-commuting* measurements — XX, YY, and ZZ parity checks akin to the Kitaev model.
But with the Floquet code stabilizing a toric code in every measurement, it “misses” the most interesting phenomenology of the Kitaev model – the fractionalization of spins and the emergence of a Majorana liquid. So, is there a way to modify the Floquet code to see this?
Yes! If one tunes the *measurement strength* of the Floquet code, one can induce coherent errors via *weak* measurements, such that the code breaks down. But it’s not into a trivial state, but something much richer. So, how do we know that there is more?
The measurement strength in the code acts similar to temperature in the Kitaev model. And indeed we find *two* signatures in the “energy” fluctuations when going to weak measurements — akin to the finite-T specific heat. The 2nd peak indicates where the qubits fractionalize!
So what’s inbetween the two peaks? A Majorana metal in which the entanglement negativity shows an L ln L scaling. Think of a long-range resonating valence bond state of the emergent Majoranas.
Publication:
Qubit fractionalization and emergent Majorana liquid in the honeycomb Floquet code induced by coherent errors and weak measurements, Guo-Yi Zhu and Simon Trebst. arXiv:2311.08450
Abstract:
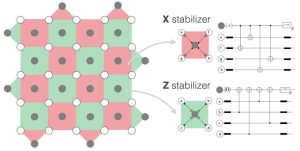
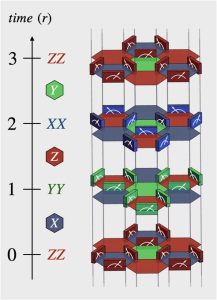
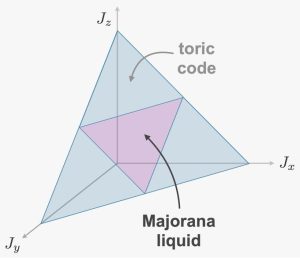
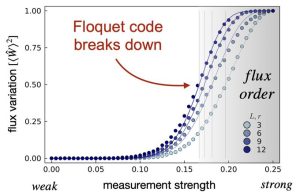
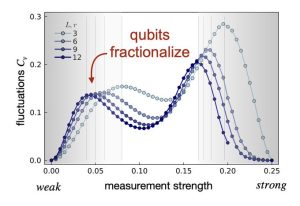
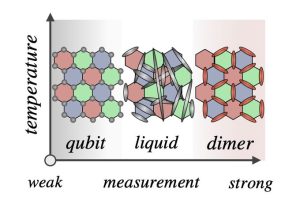
From the perspective of quantum many-body physics, the Floquet code of Hastings and Haah can be thought of as a measurement-only version of the Kitaev honeycomb model where a periodic sequence of two-qubit XX, YY, and ZZ measurements dynamically stabilizes a toric code state with two logical qubits. However, the most striking feature of the Kitaev model is its intrinsic fractionalization of quantum spins into an emergent gauge field and itinerant Majorana fermions that form a Dirac liquid, which is absent in the Floquet code. Here we demonstrate that by varying the measurement strength of the honeycomb Floquet code one can observe features akin to the fractionalization physics of the Kitaev model at finite temperature. Introducing coherent errors to weaken the measurements we observe three consecutive stages that reveal qubit fractionalization (for weak measurements), the formation of a Majorana liquid (for intermediate measurement strength), and Majorana pairing together with gauge ordering (for strong measurements). Our analysis is based on a mapping of the imperfect Floquet code to random Gaussian fermionic circuits (networks) that can be Monte Carlo sampled, exposing two crossover peaks. With an eye on circuit implementations, our analysis demonstrates that the Floquet code, in contrast to the toric code, does not immediately break down to a trivial state under weak measurements, but instead gives way to a long-range entangled Majorana liquid state.