Science Advances: Reappearance of first Shapiro step in narrow topological Josephson junctions
The state of a topological quantum bit is defined by the arrangement of two Majorana zero modes in space and time. In condensed matter, these quasiparticles that
constitute their own anti-particles can be identified at zero energy within a superconducting condensate. Within the electron-hole bound state spectrum of Josephson junctions – comprised of two superconducting leads interrupted by a short topological insulator weak link – Majorana bound states are established with a zeroenergy solution. These gapless Majorana bound states establish ultimately due to the helical spin dispersion of topological insulators as it prohibits direct backscattering, which leads to a unity probability of quasiparticles at the topological insulator to superconductor interface to undergo an Andreev reflection. Compared to Andreev bound states, the gapless Majorana bound states have a doubled periodicity with respect to the phase difference in between the two superconducting leads. This is identified by a doubling of the voltage standard of Shapiro steps, when the junction is irradiated by a radio-frequency signal.
In order to realize locally confined Majorana zero modes, the dimensionality of the topological insulator needs to be reduced from two-dimensional surfaces to a one-dimensional nanowire or nanoribbon. The authors defined Josephson junctions on topological insulator nanoribbons, which for scalability reasons have been deposited selectively in a pre-defined silicon nitride mask. The confinement of coherent states on the perimeter of the nanoribbon initially gaps the topological surface states and furthermore lifts the spin degeneracy of surface states. Therefore, quasiparticles at the nanoribbon to superconductor interface can be retro-reflected as a state of opposite momentum within the nanoribbon is available. The finite probability to be reflected will result in gapped bound states and a conventional Shapiro step response. In future experiments this can be overcome by applying an in-plane magnetic field, that restores the helical spin dispersion of the topological insulator nanoribbon
surface states.
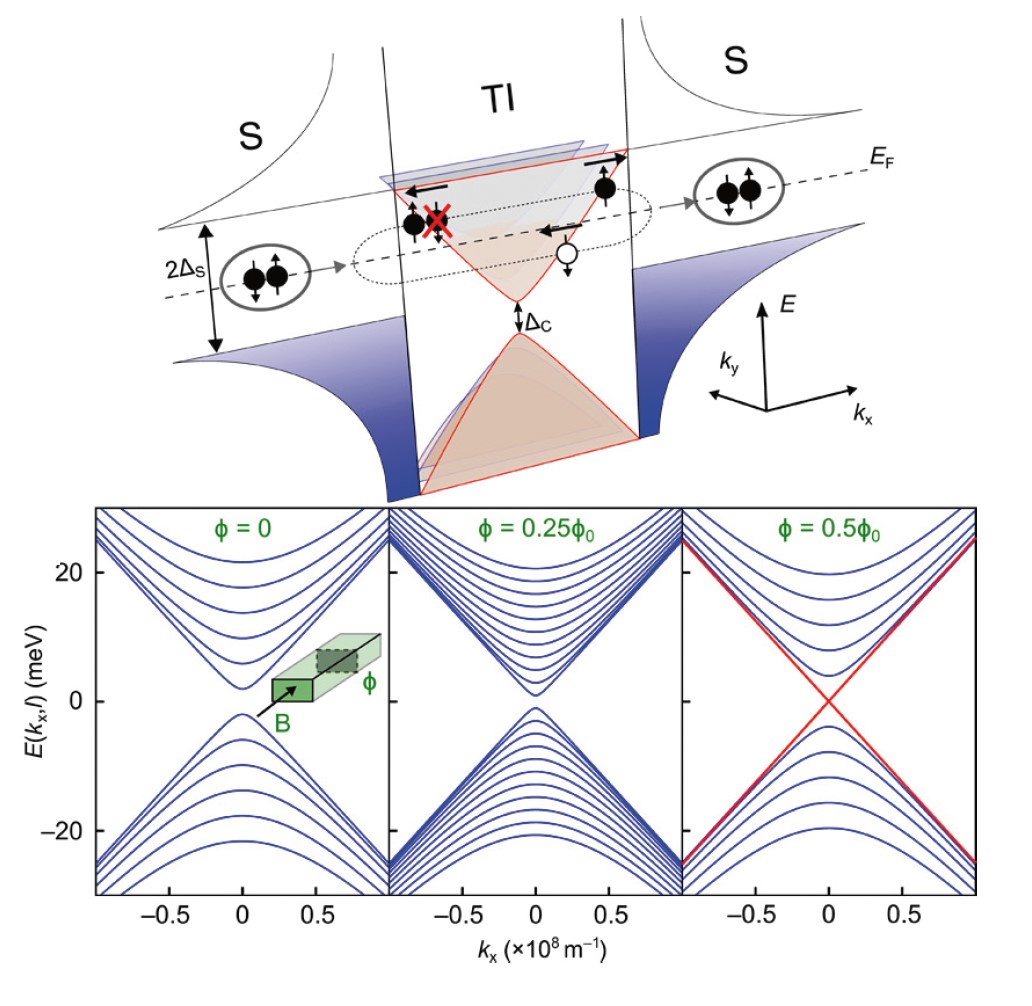
Due to the interaction of spin and momentum of topological surface charges, the otherwise spin nondegenerate surface states become doubly spin degenerate within confined topological insulator nanoribbons. Due to the spin degeneracy, the probability of quasiparticles at the interface of a topological insulator towards a superconductor to reflect becomes finite. As not every quasiparticle is being Andreev reflected, the bound state dispersion in topological insulator Josephson junctions is gapped and 2p-periodic with respect to the phase difference of the two superconducting leads of the junction.
Publication: D. Rosenbach, T. W. Schmitt, P. Schüffelgen, M. P. Stehno, C. Li, M. Schleenvoigt, A. R. Jalil, G. Mussler, E. Neumann, S. Trellenkamp, A. A. Golubov, A. Brinkman, D. Grützmacher, and T. Schäpers, Reappearance of first Shapiro step in narrow topological Josephson junctions, Science Advances 7, eabf1854 (2021)
It is the spin-momentum locking of topological surface charges that triggers Majorana bound states in Josephson junctions, but also what makes it technically so much more difficult for the same observation in confi ned nanoribbons of topological insulator materials.